Nicht wenige bezeichnen es als DAS Problem der Informatik. Mathematiker auf der ganzen Welt beißen sich die Zähne daran aus, da dessen Lösung mit einem Preisgeld von einer Millionen Dollar dotiert ist. Aber was könnte so schwer sein, dass es als „Millennium Problem“ bezeichnet wird und warum horchen IT-Fachleute rund um den Globus gespannt auf, wenn über die Lösung von P vs. NP diskutiert wird? Es geht im Grunde um die simpel erscheinende Frage: „Wo gehe ich als nächstes hin?“
Der Inhalt im Überblick
Nicht nur die Begriffe sind komplex
Das P vs. NP Problem ist ein ungelöstes Rätsel der Komplexitätstheorie. Hierbei werden von einem Computer zu lösende mathematische Probleme als P- oder NP-Probleme klassifiziert. Vereinfacht gesagt gehören alle Probleme, die effizient von einem Computer gelöst werden können, zur Klasse P. Bei NP-Problemen hingegen ist unbekannt, ob sie sich effizient lösen lassen oder nicht. Effizient bedeutet hierbei, dass die benötigte Rechenzeit eines Lösungsalgorithmus bei steigender Komplexität höchstens polynomiell (also zum Beispiel quadratisch) wächst. Klar ist aktuell nur, dass sich eine korrekte Lösung eines NP-Problems in Polynominalzeit überprüfen lässt. Ob eine Lösung in der gleichen Zeit erzeugt werden kann, ist allerdings unklar.
Der Handlungsreisende
Im Informatikstudium kommt man an der Komplexitätstheorie kaum vorbei. Will man Informatikstudenten P vs. NP erklären, wird in der Regel das Problem des Handlungsreisenden aus dem großen NP-Problemhut gezaubert.
Ein reisender Händler möchte eine möglichst kurze Handelsroute planen. Auf seiner Reise möchte er die 15 größten Städte Deutschlands besuchen und am Ende seiner Reise wieder zu Hause ankommen. Hierfür werden die Städte als Knotenpunkte auf einer Karte markiert, die Distanzen bestimmt und die Knoten sinnvoll miteinander verbunden. Was zunächst einfach klingt ist viel komplizierter als gedacht, denn es gibt unfassbare 43.589.145.600 mögliche Routen. Und das Problem gewinnt an Komplexität je mehr Städte unser reisender Händler besuchen möchte. Das macht das Problem des Handlungsreisenden zu einem der schwierigsten Problemen der NP-Klasse.
Lösungen und Beweise
Lösungsalgorithmen für NP-Probleme zu entwickeln, ist in der Regel sehr schwierig. Informatiker und Mathematiker versuchen allerdings nicht nur effektive Algorithmen zu erarbeiten. Sie versuchen außerdem zu ermitteln, ob P = NP ist. Man versucht also heraus zu finden, ob P und NP wirklich verschiedene Problemklassen sind oder ob es möglich ist NP-Probleme auch in Polynominalzeit zu lösen. Wissenschaftler auf der ganzen Welt versuchen allerdings zu beweisen, dass P != NP gilt. Woran liegt das? Sind die klugen Köpfe dieser Welt nicht daran interessiert, komplexe Probleme genauso schnell zu lösen wie weniger komplexe Probleme? Und für wen sind all diese Theorien, Überlegungen und Beweise überhaupt relevant?
Das Ende der Kryptographie
Der Grund, warum sich Fachleute wünschen, dass NP-Probleme nahezu unlösbar bleiben, heißt Kryptographie. Im Gegensatz zu vielen anderen Bereichen ist Komplexität in der Kryptographie nicht nur erwünscht, sondern notwendig. Hierzu muss man wissen, dass die meisten heute angewendeten Verschlüsselungsverfahren einzig und allein darauf beruhen, dass der Aufwand den verwendeten Schlüssel zu „erraten“ zu hoch ist. Das Problem des „Erratens“ ist also ein NP-Problem. Nicht nur theoretisch, sondern auch praktisch bedeutet somit der Beweis der Lösbarkeit von NP-Problemen das Ende sämtlicher aktuell verwendeter Verschlüsselungsverfahren.
Allen, den das Mittagessen nun im Halse stecken geblieben ist, sei hier aber gesagt: Es gibt auch weiterhin Hoffnung für die Kryptographie. Das NP-Problem wurde schon oft vermeintlich gelöst. Sowohl P = NP als auch P != NP wurden schon oft bewiesen. Allerdings stellte sich bisher jede einzelne Lösung und jeder einzelne Beweis als falsch oder nicht nachvollziehbar heraus. Es kann also aufgeatmet werden. Das größte Rätsel der Informatik bleibt auch weiterhin ungelöst.
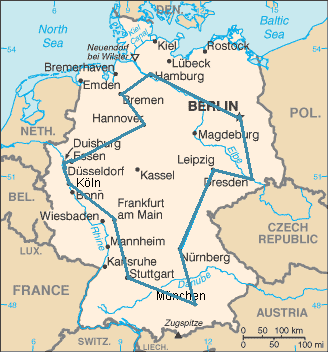
Quelle: Wikipedia, TSP Deutschland 3.png; Lizenz: Gemeinfrei
Zum Schluss soll nun noch die womöglich brennendste Frage dieses Artikels beantwortet werden. Unser in Hamburg ansässiger reisende Händler wählt am besten diese Route: Hamburg – Berlin – Dresden – Leipzig – Nürnberg – München – Stuttgart – Frankfurt – Köln – Düsseldorf – Duisburg – Essen – Dortmund – Hannover – Bremen – Hamburg.






Danke, ein sehr gut geschriebener Beitrag!
Interessant, aber es muss heißen polynomial, nicht polynominal, weil es ja von Polynom und nicht von Nomen abgeleitet ist :)
Super Artikel, nur wäre es doch kein Problem für die Kryptographie P = NP bewiesen würde oder? Ich meine, dass jede Verschlüsselungsmethode irgendwie irgendwann geknackt werden könnte ist doch einleuchtend? Es geht ja nur darum, dass es so lange dauern würde, dass es wieder sicher ist, also würde der Beweis keinen Unterschied machen oder?
Ja und nein – bisher wurden alle Verschlüsselungsmethoden geknackt, da sie entweder Konstruktionsfehler beinhalteten, weshalb sie angreifbar waren, oder durch schiere Rechenpower, das heißt man war für die gewählte Problemschwierigkeit irgendwann in der Lage einfach alles in absehbarer Zeit auszuprobieren.
Wenn wir nun an den Punkt kommen, dass P = NP ist, dann heißt das, dass (nahezu) jeder heute gängige Verschlüsselungsalgorithmus auf einem einfach zu lösenden Problem beruht. Und damit wird diese Verschlüsselung (näherungsweise) wirkungslos und wir bräuchten komplett andere Verschlüsselungsalgorithmen
Wäre nicht: Hamburg – Bremen – Hannover – Dortmund – Essen – Duisburg – Düsseldorf – Köln – Frankfurt – Stuttgart – München – Nürnberg – Leipzig – Dresden – Berlin Hamburg besser? ;-)
Nein, denn ein echter Hamburger setzt seinen Fuß nur nach Bremen, wenn es nicht mehr anders geht ;)
Könnte man nicht anhand der Größe des Raumes auch beachten bei einer evtl. Gleichung?